www.plusplanet.de
Schulinfos von F. Töns
Schulinfos von F. Töns
- Willkommen
- PJK Webdesign (SJ 23/24)
- Mathe_Q2_GK_Abi2024
- Mathe_LK_Abi2024
- Informatik_Q2_Abi2024
- Informatik Klasse 6 (SJ 22/23)
- Mathe_7b_(Schmidt)
- Informatik_EF_Abi2025
- Projektkurs Webdesign (SJ 22/23)
- Mathematik_Q2_Abi2023
- Informatik_EF_Abi2024
- Informatik_Q2_Abi2022
- Mathematik_LK_Q2_Abi2022
- Mathematik_EF_Abi2023
- Informatik_EF_Abi2023
- Mathematik_Q2_Abi2021
- Mathematik_EF_Abi2022
- Informatik_Q2_Abi2020
- Lösungsarchiv
- Verschiedenes
- Impressum
Willkommen auf www.plusplanet.de
Bitte wählt links euren Kurs aus!12.02.2024
Projekttage "GreenIT"https://zumpad.zum.de/
20240213_toe_projekttage
20240213_toe_datenbank
16.11.2023
Login für den Informatik-Biberhttps://wettbewerb.informatik-biber.de/index.php?action=login
02.11.2023
Heutige Themen• Informatiksysteme
• Der PC
• Der Dateimanager
Eine Ordnerstruktur für unsere Schulfotos:
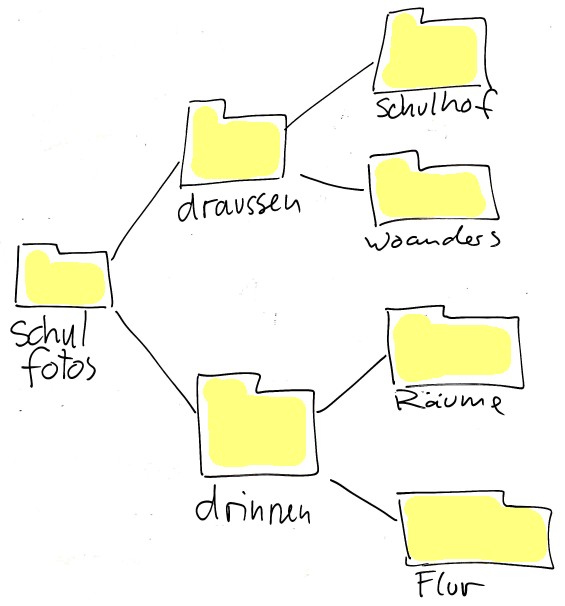
26.10.2023
Vertretungsunterricht für Klasse 6Caesar-Verschlüsselung
20220828_225218_tn.jpg
Verschlüssele eine Nachricht (z.b. dein Leibgericht), indem Du das Alphabet um drei Stellen verschiebst (aus "a" wird "D"). Dein Nachbar soll die Nachricht wieder entschlüsseln.
Übung zum Entschlüsseln (Verschiebungszahl unbekannt):
"Warum hat das Flugzeug einen Propeller", möchte der Lehrer wissen.
"Damit der Pilot nicht schwitzt", antwortet Fritzchen.
"So ein Unsinn, das ist ja völlig falsch."
"Komisch", erwidert Fritzchen, "PJO ZHO LPUTHS, DPL PU LPULT MSBNGLBN KLY WYVWLSSLY HBZNLMHSSLU PZA. KH OHLAALU ZPL THS ZLOLU TBLZZLU, DPL KLY WPSVA NLZJODPAGA OHA."

Warum läuft die Krankenschwester auf Zehenspitzen am Medikamentenschrank vorbei?
Fvr zöpugr qvr Fpuynsgnoyrggra avpug nhsjrpxra.
Wo schlafen Katzen wenn es dunkel wird?
Va qre Zvrmjbuahat!
Was macht Robin Hood mit gestohlenen Deo-Rollern?
Re iregrvyg fvr hagre qra Nezra.
Warum erhalten Polizisten in Zukunft eine große Schere für Ihre Polizeiausrüstung?
Qnzvg fvr qra Oöfrjvpugra qra Jrt nofpuarvqra xöaara.
Wie kann man 1 Liter Wasser in einem Sieb transponieren?
Vaqrz zna qnf Jnffre ibeure rvasevreg!
Kann man mit einem deutschen Personalausweis nach Istanbul fliegen, um dort Urlaub zu machen?
Arva, zna oraögvtg rva Syhtmrht!
Welche Handwerker essen am meisten?
Znhere! Qvr irechgmra tnamr Uähfre.
Welche Schuhe haben keine Sohlen, berühren nicht den Boden und passen an keine Füße?
Qvr Unaqfpuhur
Was kommt raus, wenn man eine lange Schlange mit einem Igel kreuzt?
Fgnpuryqenug
Was steht auf dem Grabstein des Mathelehrers?
Qnzvg ung re avpug trerpuarg.
Schreibe selbst eine Nachricht darüber, wohin du gern in Urlaub fahren würdest. Wähle die Verschiebungszahl selbst aus. Dein Nachbar soll deine Verschlüsselte Nachricht "knacken".
19.10.2023
Vertretungsunterricht für Klasse 6Maustraining:
https://maustraining.zawiw.de/level/0
• Tastaturtraining: Erstelle in Notepad++ eine Kopie von folgenden kleinen Bildchen:
Diese drei Bildchen, welche nur aus Zeichen bestehen, nennt man auch "ASCII-Art". Erstelle selbst ein Gesicht nur aus Zeichen.
Mit Fingern zählen:
https://www.youtube.com/watch?v=OkcVk_PGYL4